La paradoja del cuadrado perdido es una ilusión óptica usada en clases de matemáticas, para ayudar a los estudiantes a razonar sobre las figuras geométricas. Está compuesta de dos figuras en forma de triangulo de base 13 y altura 5, formadas por las mismas piezas, donde uno aparenta tener un "agujero" de 1×1 en él.
La clave de la paradoja está en el hecho de que ninguno de los triángulos tiene la misma área que sus piezas componentes. El área de cada pieza es:
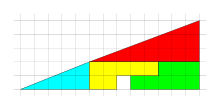
Pieza 1: Un triángulo rectángulo de base 8 y altura 5.
Pieza 2: Otro triángulo rectángulo de base 5 y de altura 2.
Pieza 3: Un rectángulo de base 5 y altura 2 al que le faltan 2 cuadrados.
Pieza 4: Otro rectángulo de base 5 y altura 2 al que le faltan 3 cuadrados.
Con las cuatro piezas podemos construir dos figuras con forma de triángulo rectángulo de base 13 y altura 5 pero en uno de los triángulos (figura 2) falta un cuadrado.
Explicación
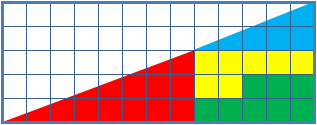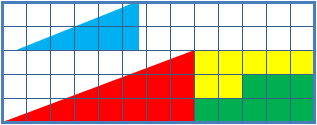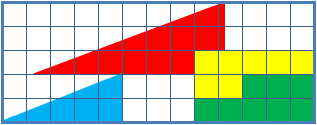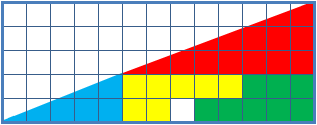
En realidad las dos figuras que se obtienen con las cuatro piezas no son triángulos rectángulos. Con una regla podemos ver que en los dos casos la supuesta hipotenusa no es una línea recta y que está formada por dos líneas que tienen una pendiente ligeramente distintas. Por superposición podemos ver que las dos piezas con forma de triángulo rectángulo no tienen el mismo ángulo.
Las dos figuras formadas con las cuatro piezas tienen que tener el mismo área. Si superponemos el primer "triángulo rectángulo" sobre el segundo (al que le falta el cuadrado) vemos que queda sin cubrir una parte. La diferencia no es muy grande pero se corresponde con el área del cuadrado que falta.


hola mayra la verda me gusto mucho tu tema se me hace muy llamativo e interesante , no se si me podrias mandar mas enlaces para conseguir mas información , de antemano gracias
ResponderEliminar