Desapariciones Geometricas

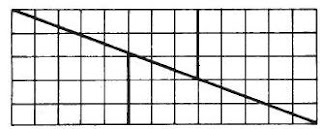
• En el primer rectángulo aparecen 65 cuadrados (5 por 13). 
• Si se recorta este rectángulo siguiendo las líneas marcadas y, con los trozos se reconstruye un cuadrado como se indica, al calcular el área de la nueva figura, es de 8 unidades por 8, es decir, hay sólo 64 cuadrados. 
• ¿Dónde ha quedado el que falta? 
• La aparente pérdida de superficie es debida al reajuste de los trozos. 
• De hecho, en la última figura, los bordes no coinciden exactamente, sino que forman un pequeño paralelogramo, casi imperceptible, y no un cuadrado perfecto. 
• Esto sería evidente si la figura fuera más grande y estuviera construida con sumo cuidado. 
• Las sorpresas de este tipo se llaman paradojas de Hooper.

• Desde un punto de vista más teórico, debe notarse que las desapariciones de superficie hacen intervenir, en muchas ocasiones, segmentos de recta cuyas longitudes forman una serie de Fibonacci, es decir, una sucesión en la que cada término es la suma de los dos precedentes: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,... 
• Las propiedades fundamentales de esta serie es que, si uno de los números que la constituye se eleva al cuadrado, este número será igual al producto de los dos números situados delante y detrás de él, más o menos una unidad. Así 8 x 8 = 64 y 5 x 13 = 65