Curiosidades

Teorema de Pitágoras

Antes de comenzar a hablar del Teorema de Pitágoras es interesante preguntarse ¿Quién es Pitágoras? Pitágoras de Samos fue un filósofo y matemático griego nacido en el año 569 a.C. considerado el primer matemático puro de la historia. Contribuyo bastante en el avance de la matemática helénica, la geometría y aritmética.

Historia del Teorema de Pitágoras

El Teorema de Pitágoras tiene ese nombre porqué su demostración es esfuerzo de la escuela de pitagórica. Anteriormente, en Mesopotamia y el antiguo Egipto se conocían ternas de valores que se correspondían con los lados de un triángulo rectángulo, y se utilizaban para resolver problemas referentes a los citados triángulos, tal como se indica en algunas tablillas y papiros.
Sin embargo, no ha perdurado ningún documento que exponga teóricamente su relación. La pirámide de Kefrén, fue la primera gran pirámide que se construyó basándose en el llamado triángulo sagrado egipcio, de proporciones 3-4-5. Las novedades más importantes que registran los textos babilónicos se refieren a la solución algebraica de ecuaciones lineales y cuadráticas y el conocimiento de llamado Teorema de Pitágoras.

Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las respectivas longitudes de los catetos.


                                     
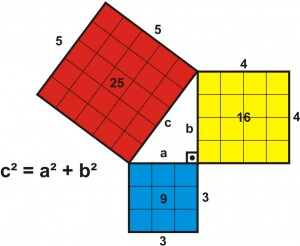
Si en un triángulo rectángulo hay catetos de longitud A y B y la medida de la hipotenusa es C entonces se cumple la siguiente relación

                                                            
De esta ecuación se deducen  tres corolarios de verificación algebraica y aplicación práctica:

${\displaystyle b={\sqrt {c^{2}-a^{2}}}}$

${\displaystyle c={\sqrt {a^{2}+b^{2}}}}$

El Teorema de Pitágoras es uno de los que cuenta con más demostraciones, utilizando métodos diferentes, esto se debe a que en la edad media se exigía una nueva demostración del teorema para alcanzar el grado de “Magister Matheseos”.
Si bien este teorema ha quedado demostrado matemáticamente en diferentes ocasiones, no solo se quedó allí, el Teorema de Pitágoras tiene muchas aplicaciones en la vida real, en la arquitectura y construcción por ejemplo es la aplicación más obvia de este teorema, pues cuando se está trabajando con tejados en formas triangulares, este teorema se aplica cuando se trabaja con triángulos rectángulos o triángulos con un ángulo de 90°.

Son muchas las aplicaciones
                                               
Es de este teorema en la vida diaria, pero a veces no nos damos cuenta, en la navegación es muy utilizado, pues la triangulación es un método muy utilizado para señalar una ubicación cuando se conocen dos puntos de referencia, cuando esta triangulación se emplea sobre un ángulo de 90° se usa el Teorema de Pitágoras, también en la triangulación de celulares es muy usada. Dicho teorema tiene otras aplicaciones como en la localización de terremotos, investigación de una escena de un crimen y trayectoria de un misil o una bala.

Teorema de Pitágoras ejercicios y solución.

Problema 1

Calcular la hipotenusa del triángulo rectángulo de lados 3cm y 4cm.

 Los lados son

$$a=3cm,b=4cm$$ Aplicando el teorema de Pitágoras,

Por tanto, la hipotenusa mide 5cm.

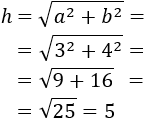
Problema 2

Si la hipotenusa de un triángulo rectángulo mide 2cm y uno de sus lados mide 1cm, ¿cuánto mide el otro lado?
Llamamos a los lados a y b y a la hipotenusa h.
 Sabemos que                                                                                h=2 , a=1
Por Pitágoras, sabemos que                                                           h2=a2+b2

Sustituyendo los valores conocidos tenemos que

Ahora despejamos b en la ecuación

Hemos escrito los signos positivo y negativo porque es lo que, en teoría, debemos hacer. Pero como b representa la longitud de un cateto, no puede ser un número negativo.
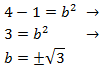
Por tanto, el cateto mide

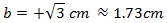
Podemos dejar la raíz cuadrada o aproximarla.

Problema 3

Calcular la altura del siguiente triángulo sabiendo que sus lados miden 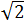, 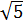y su base 3.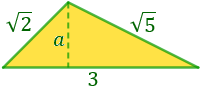

Para poder calcular la altura del triángulo, a, tenemos que dividirlo en dos triángulos rectángulos (para poder aplicar el teorema de Pitágoras).
Los dos triángulos son los siguientes:

La base del triángulo (que mide 3) se divide en dos (la base de cada triángulo). No sabemos cuánto mide cada base, pero sí que sabemos que

$$x+y=3$$

Aplicamos Pitágoras al primer triángulo y obtenemos la ecuación:

Notemos que no conocemos ninguno de los dos catetos.
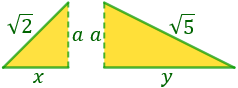
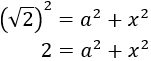
Procediendo del mismo modo para el otro triángulo, obtenemos

Es decir, tenemos las siguientes ecuaciones:

Podemos aislar la y en la tercera ecuación, obteniendo

En la segunda ecuación tenemos una y, que sabemos que es 3 - x, así que sustituimos en ella:

Como tenemos una resta al cuadrado, aplicamos la fórmula del binomio de Newton, que recordamos que es

Por tanto,

Ahora despejamos a ²

Recordemos que también teníamos la ecuación

Despejamos también en ella a ²

Es decir, las dos ecuaciones que tenemos son

Y como a ² = a ², podemos igualar ambas expresiones obteniendo una ecuación de primer grado

Sabiendo el valor de x podemos obtener el de y

Ya sabemos cuánto mide cada base y podemos ahora calcular la altura.
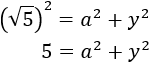
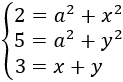
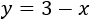
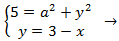
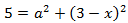
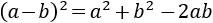
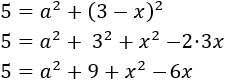
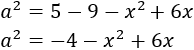
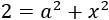
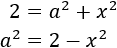
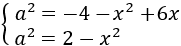
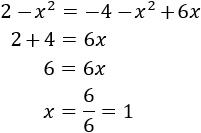
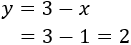
La primera de las ecuaciones era

Como sabemos que x = 1 tenemos que

Y como $a$
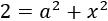
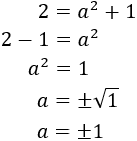
es la altura, no puede ser negativa. Por tanto, la altura del triángulo es

$$a=1$$